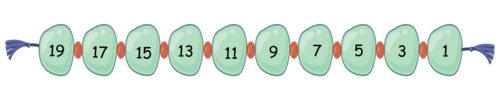Place value System
Welcome to Class 1 Place value System lesson plan
Learning Objectives
- Origin of Numerals
- Introduction to place value up to 3 digits
- Comparing two 2-digit numbers
- Partitioning two- and three-digit numbers
- Know the value of numbers
- Ascending and descending order
Origin of Numerals
Knowledge of number skills is extremely valuable for us to perform many activities of our daily lives. We use them so often that it appears as though they have always existed. Have you ever wondered
- When was it that man first start counting?
- In what ways did he represent numbers?
- Did all people all over the world count in the same way?
Let’s try to find answers to some of these questions.
Indeed, counting is a pretty old. The numbers we know now have been in use for a long time. But how do we know that? Information about past times is obtained in a few ways.
- told by their elders and teachers
- written on palm leaves
- writings on stones found in temples or caves
- noted in the records of ancient travellers
Using examining such evidences our scholars and scientists have understood that the modern numbers used in the world have first existed in India. There are a few evidences which show that modern numeral systems evolved from India.
- Vedas describe about numbers.
- An Arabic traveller by the name Abu al Khwarizmi recorded his visit to India about 1200 years ago. He noted down in his book that Indians had a
- well-developed number system
- calculation methods
- zero in their numeral system
Now we understand how numbers and counting has been an age-old practice in India.
Digits (Numbers) and Arrangement
Symbols of Numbers
In the Indian (also called Hindu) system of writing numbers there are only ten symbols. For the numbers one to nine the symbols are called Anka (meaning “mark”). The zero symbol is called shunya (meaning “empty”). These ankas (digits) used for all calculations in the world are called “Hindu-Arabic” numbers.
As writing evolved the symbols are used to count and write from shunya to nine. They form the one-digit numbers or Units.
Place-value of Numbers
Tens and More…..
But how do we write ten after nine? When we have more than nine things to count, we start writing in a new column one place to the left of the anka. Thus, one place to the left of units or one-digit place we start a new column called the “tens”.
| Tens | Units |
Now we know that we have more things to count, so let’s keep the ten as a group in the tens column and add more digits in the units or ones’ place.
Number 32 has ________ Tens and _______ Ones and Number 14 has ______ Ten and ______ Ones
| Tens | Ones |
| Tens | Ones |
Activity: Make a number
Number Exercise: Identifying places in a number.
| Tens Place | Units Place | Write the number |
|---|---|---|

|

|
31 |

|

|
55 |

|

|
|

|
||

|

|
|

|
||

|

|
|

|
||

|
||

|
Activity: Partition a number
Number Exercise – Partition a two-digit number into individual places
| Color Tens place green | Color the units place red | Number |
|---|---|---|

|

|
54 |

|

|
56 |

|

|
49 |

|

|
81 |

|

|
95 |

|
07 |
| Color Tens place green | Color the units place red | Number |
|---|---|---|

|
|
38 |

|
10 | |
|
|
26 |

|
02 |
Activity: Finding the place-value
Number Exercise – Identify the ones and tens place of a number.
| What is in the ones place in each number? | |||||||
26
|
31
|
10
|
53
| ||||
| 65
|
12
|
44
|
39
| ||||
| 20
|
7
|
88
|
74
| ||||
| What is in the tens place in each number? | |||||||
40
|
96
|
18
|
63
| ||||
| 9
|
47
|
59
|
75
| ||||
| 25
|
11
|
5
|
33
| ||||
| Circle all numbers having zero in the ones place
25 68 90 56 92 30 29 41 | |||||||
| Circle the numbers having 5 in the tens place
52 95 30 59 18 5 91 85 | |||||||
Numbers have a value
Numbers – Are they more or less?
Activity: Farm Fresh
Number Exercise – Count and Compare Numbers
Count and write the number. Tick whichever is more.
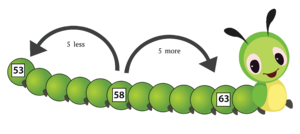
Numbers - More or Less (By 1s, 2s, 5s)
Write the numbers in sequence. By how many more or less are the numbers in the boxes.
Activity: Find the counting pattern
Number Exercise: Counting by 2s, 3s and 5s
Find or write the given skip counting pattern.
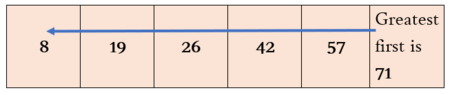
Ascending and Descending Order of Numbers
We have seen that numbers have value based on the place in which they are present. Many times, we come across smallest and greatest of a given set of numbers in our activities.
For example, would you like to eat more or less of your favourite dish? Would you like to drink more or less of a cough medicine?
Ganesha likes to have more modakas. Help Ganesha choose the order of plates and colour the picture.
There are 6 plates having following number of modakas.
Ganesha says
“hmm… give me the plates having a smaller number of modakas first”.
So, how do you choose the order? Find a plate with the smallest number of modakas, then next smaller number and so on….
Ascending Order - numbers increasing in value from smallest to largest
Consider Bhima, who eats lots of food. He was also a great cook. He would say,
“hmm… give me the plates having greatest number of modakas first”.
Now, how do you choose serve him? You should find a plate with the greatest number of modakas first.
Descending Order – numbers decreasing in value from largest to smallest.
Place-value of Three-Digit Numbers
Hundreds and More….
When we have more than 99 things to count what should we do?
Simple, we start our digits in a new column one place to the left of the anka (digit) in the tens place. A place left to the tens place is called the “hundreds place”.
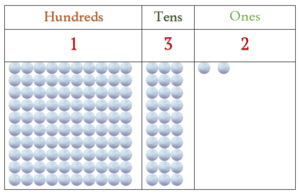
| Hundreds | Tens | Units |
| 1 | 1 | ० |
Now, we show how many hundreds, tens and ones we have in each place respectively. Using this we can write as many numbers as we want now…
Number 132 has 1 Hundred 3 Tens and 2 Ones
What if we have zero in the tens place?
| Place | Hundreds | Tens | Units |
| Value | most | more | less |
| 100 | 10 | 1 |
- The number system is based on ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). It is called Decimal Number System.
- Place or position of the digits goes from right to left starting from units, then tens place to the left of units, then hundreds place to its left.
- The value of a number remains the same at all times.
- Value of the number is 10x times more as we go left from the units’ place.
- Using this system large and small numbers can be written easily.
Order of Numbers (Ascending and Descending)
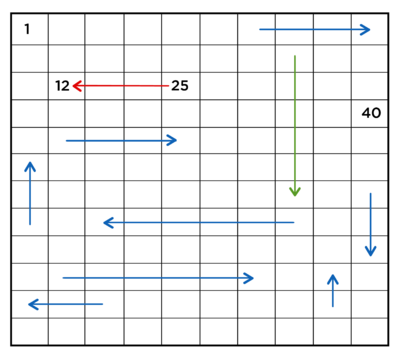
Harish was playing football in his school. He made the following moves with the ball in the field. Count and write the numbers in the squares where the arrow starts and ends. Count according to the spaces moved forward or backwards.
- He moved forward by 5 boxes from ______________ to ____________
- He moved forward by 10 boxes from ____________ to _____________
- Find the highest number box touched by the ball? ________________
- Find the lowest number box touched by the ball? ________________
- What is the last number in the field? _________________
Activity: Finding the Place-value
Number Exercise – Identify the ones, and tens place of a number.
Activities and Exercises
Activity 1
Draw on ground big squares (1 to 30) for pairs of students to play. One student is tagged units and the other tens and both are far apart. Teacher calls out a one- or 2-digit number. Students should instantly identify their units or tens tag and reach those squares within time. When the student group is large pair of students can be assigned specific 1 -10 rows in which the pair has to join when the number is called out.
Activity 2
Ten students are assigned 10 digits of units’ place (wearing a digit flash card). Another set of 10 students are assigned 10 digits of 10s place (wearing a digit flash card). The students form a circle randomly around the basket containing rubberbands. When a number is called those students join to form a pair in the middle and collect the rubberbands of their friend’s digit.
Suns and Blackholes
Choose any three skip countings for a game – 2s, 4s, 3s, 5s, 6s etc before game starts. Draw squares on the ground (1 to 40) marking suns and blackholes on random squares. Game can be played by 2 to 4 students simultaneously. First time display flash cards with any number below 20 and the child stands in that square. Subsequently call out “move by 3” all students in the square move forward by 3. Then say “move by 5” they count from their squares and move to that number. If they encounter a sun they additionally move 4 squares as bonus. If they encounter a black hole they move exactly by 10 backwards. At least 2 different skip counts may be used in one game and one skip count for bonus.
Exercises
Skip Counting Charts.
Count by 2s and color them orange.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 42 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
Count by 3s and color them yellow.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 42 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
Count by 5s and color them green.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 42 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
When even number is called out one student marks the square with that number, Odd number is identified and marked by another student.
| 1 | 6 | |||||||||
| 39 | ||||||||||
| 51 |
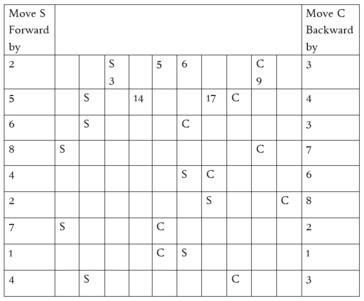
Find Surya and Chandra in each row and their meeting point by counting backwards and forwards. Write the numbers and color boxes as shown in the grid starting from 1 ending at 99. This can be a field activity also for children.
Surya and Chandra are represented in each row by S and C.
1. Identify the number in the grid on which they are located. Example row 1, Surya is on number 4 and Chandra on number 9.
2. The number by which Surya has to be moved forward is given on the left
3. The number by which Chandra has to be moved backwards is given on the right.
4. Example – Count forward by 2 from 3 to 5 for Surya and color that cell yellow. Similarly count backwards by 3 from 9 to 6 for Chandra and color that cell green.
5. Repeat this process for each row and find the pattern.