Difference between revisions of "Shulbasutras (शुल्बसूत्राणि)"
(adding content and references) |
m |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Shulbasutras (Samskrit: शुल्बसूत्राणि) are manuals for the construction of yajnas. They are sections of the Kalpasutras, associated in particular with the Shrautasutras. Each Shrautasutra seemed to have their own Shulbasutra section based on literary data; however, in the present days, only seven of these sutra works, Baudhayana, Apastamba, Katyayana, Manava, Maitayana, Varaha and Vadhula are available. | |
| − | + | == परिचयः ॥ Introduction == | |
| − | |||
| − | == Introduction == | ||
Recognized as the oldest and earliest treatises on mathematical problems, Shulbasutras give us a glimpse of the knowledge of geometry that the vedic people possessed. Incidentally they furnish us with a few other subjects of much mathematical interest.<ref name=":0">Datta. Bibhutibhusan, (1932) ''The Science of the Sulba. A Study in Early Hindu Geometry.'' Calcutta: The University of Calcutta</ref> | Recognized as the oldest and earliest treatises on mathematical problems, Shulbasutras give us a glimpse of the knowledge of geometry that the vedic people possessed. Incidentally they furnish us with a few other subjects of much mathematical interest.<ref name=":0">Datta. Bibhutibhusan, (1932) ''The Science of the Sulba. A Study in Early Hindu Geometry.'' Calcutta: The University of Calcutta</ref> | ||
| Line 10: | Line 8: | ||
== Authors and Commentators == | == Authors and Commentators == | ||
Unlike the other Sutra charanas, there are a very few Shulbasutra texts available at present and all of them belong to Yajurveda. The Shulbasutras of Baudhayana, Apastamba, Katyayana and Manava are the main sources of the knowledge of geometry. The Kalpa texts of Vedangas clearly outline that astronomy on one hand and geometry on the other were cultivated under different circumstances by different rtviks based on the duties apportioned to them in the conduct of yajnas.<ref name=":2">Bag, A. K., (1979) ''Mathematics in Ancient and Medieval India.'' Varanasi: Chaukhambha Orientalia. (Pages 103 - 174)</ref><ref name=":0" /> | Unlike the other Sutra charanas, there are a very few Shulbasutra texts available at present and all of them belong to Yajurveda. The Shulbasutras of Baudhayana, Apastamba, Katyayana and Manava are the main sources of the knowledge of geometry. The Kalpa texts of Vedangas clearly outline that astronomy on one hand and geometry on the other were cultivated under different circumstances by different rtviks based on the duties apportioned to them in the conduct of yajnas.<ref name=":2">Bag, A. K., (1979) ''Mathematics in Ancient and Medieval India.'' Varanasi: Chaukhambha Orientalia. (Pages 103 - 174)</ref><ref name=":0" /> | ||
| + | |||
| + | === List of Shulbasutra Works === | ||
| + | Of the available extant texts, Baudhayana Shulbasutra is considered to be the most ancient one. Following is the list of shulbasutras and their commentators. | ||
{| class="wikitable" | {| class="wikitable" | ||
!Vedas | !Vedas | ||
| Line 28: | Line 29: | ||
|Purvabhaga (7 Kandikas with 90 Sutras) | |Purvabhaga (7 Kandikas with 90 Sutras) | ||
Uttarabhaga (40 or 48 shlokas) | Uttarabhaga (40 or 48 shlokas) | ||
| − | |Rama or Ramachandra (Shulba-sutra-vrtti) | + | |Rama or Ramachandra (Shulba-sutra-vrtti), Shulbasutravivarana (Mahidhara), Karka (Shulbasutrabhashya) |
|- | |- | ||
! rowspan="7" |Krishna Yajurveda | ! rowspan="7" |Krishna Yajurveda | ||
| rowspan="4" |Taittriya | | rowspan="4" |Taittriya | ||
|'''Baudhayana''' | |'''Baudhayana''' | ||
| − | |3 Adhyayas | + | |3 Adhyayas (about 520 Sutras) |
|Dvarakanatha Yajva (Sulba-dipika), Venkatesvara Dikshita (Shulba-mimamsa) | |Dvarakanatha Yajva (Sulba-dipika), Venkatesvara Dikshita (Shulba-mimamsa) | ||
|- | |- | ||
|'''Apastamba''' | |'''Apastamba''' | ||
|6 Patalas (21 Adhyayas and 223 Sutras) | |6 Patalas (21 Adhyayas and 223 Sutras) | ||
| − | |Kapardisvami (Shulba-vyakhya), Karavindasvami (Shulba-pradipika), Sundararaja (Shulba-pradipa or Sundararajiya), | + | |Kapardisvami (Shulba-vyakhya), Karavindasvami (Shulba-pradipika), Sundararaja (Shulba-pradipa or Sundararajiya), Gopala (Shulbabhashya) |
|- | |- | ||
|Varaha | |Varaha | ||
| Line 75: | Line 76: | ||
|} | |} | ||
| − | == Etymology == | + | === Qualities of a Shulbakara === |
| − | The word Shulba (शुल्ब) means a 'cord', 'a rope', 'a string'. A Sutra refers to a short rule. The commentators refer to this subject matter as Shulba as the true name, Shulba-parishista, Shulbi Kriya etc.<ref name=":0" /> | + | Mahidhara in his commentary on Katyayana shulbasutra succintly describes the qualities of a Shulbakara.<ref name=":1">Prof. K. Ramasubramaniam's Lectures - ''Vedas and Sulbasutras, Parts 1 and 2''</ref><blockquote>सङ्ख्याज्ञः परिमाणज्ञः समसूत्रनिरञ्छकः । समसूत्रौ भवेद्विद्वान् शुल्बवित् परिपृच्छकः।।</blockquote><blockquote>शास्त्रबुद्धिविभागज्ञः परशास्त्रकुतूहलः। शिल्पिभ्यः स्थपतिभ्यश्चाप्याददीत मतीः सदा।।</blockquote><blockquote>तिर्यङ्मान्याश्च सर्वार्थः पार्श्वमान्याश्च योगवित्। करणीनां विभागज्ञः नित्योद्युक्तश्च सर्वदा।।</blockquote>A shulbakara must be versed in arithmetic, versed in mensuration, must be an inquirer, quite knowledgeable in one's own discipline, must be enthusiastic in learning other disciplines, always willing to learn from practicing sculptors and architects... and one who is always industrious. |
| + | |||
| + | Besides having the above qualities, Shulbakaras had to perform several other important duties systematically viz., | ||
| + | * to clean and level a plot on which the altar is to be constructed | ||
| + | * to fix the east-west line (prachi) for it was considered as the reference line | ||
| + | * to construct bricks of specific sizes | ||
| + | * to draw diagrams of specific sizes on the level ground on which the altar is to be constructed | ||
| + | * to lay bricks subject to certain principles | ||
| + | |||
| + | == व्युत्पत्तिः॥ Etymology == | ||
| + | The word Shulba (शुल्ब) means a 'cord', 'a rope', 'a string'. A Sutra refers to a short rule. The commentators refer to this subject matter as Shulba as the true name, Shulba-parishista, Shulbi Kriya etc. | ||
| + | |||
| + | In few other instances the word "rajju (रज्जुः) has been used. B. B. Datta states that the words "shulba (शुल्ब)" "shulva (शुल्व)" and "rajju (रज्जुः) may be used synonymously to mean a rope or cord.<ref name=":0" /> | ||
| − | + | The word "shulba or shulva" (sulva) stems from the dhatu "शुल्ब्" used in the meaning "माने । to measure" and hence its etymological significance is "measuring" or act of measurement. The term Shulba can be presented in the following ways<ref name=":1" /> | |
| − | # | + | # भावव्युत्पत्तिः - शुल्बनम् इति शुल्बः । the act of measuring (mensuration) |
| − | # | + | # कर्मव्युत्पत्तिः - शुल्बयते इति शुल्बः । the entity/result obtained by measuring (line) |
| − | # | + | # करणव्युत्पत्तिः - शुल्बयत्यनेन इति शुल्बः । the instrument of measuring |
| − | + | In the Shulbas the measuring tape is called "Rajju", so is "a line". One who is well-versed in the science of Shulba (geometry) is called Shulbavijnana, a Shulbavid (expert in geometry), a Sulbapariprcchaka (an inquirer into the Shulba), a Samkhyaajna (expert in numbers), Parimaanajna (expert in measuring). A special term sama-sutra-niranchaka (meaning uniform rope stretcher) is also used, this rope plays a very significant role and we find many references of similar words rajjuka, rakku-grahaka, sutra-grahaka - all used to denote a maharaja's land surveyor. A sutra-grahaka is further described as an expert in alignment, a rekajna, one who knows "the line".<ref name=":0" /> | |
| − | In the Shulbas the measuring tape is called "Rajju", so is "a line". One who is well-versed in the science of Shulba (geometry) is called Shulbavijnana, a Shulbavid (expert in geometry), a Sulbapariprcchaka (an inquirer into the Shulba), a Samkhyaajna (expert in numbers), Parimaanajna (expert in measuring). A special term sama-sutra-niranchaka (meaning uniform rope stretcher) is also used, this rope plays a very significant role and we find many references of similar words rajjuka, rakku-grahaka, sutra-grahaka - all used to denote a maharaja's land surveyor. A sutra-grahaka is further described as an expert in alignment, a rekajna, one who knows "the line". | ||
It is extremely interesting to note that land surveying is an ancient procedure followed by our ancestors. | It is extremely interesting to note that land surveying is an ancient procedure followed by our ancestors. | ||
| − | == | + | == Mathematical References in Vedas == |
| − | Yajnas are of two main classes: Nitya (obligatory) and Kamya (optional or performed with a special intent). | + | The existence of numbers, their usage, the decimal system being in vogue, the concept of infinity are unambiguously presented in the following examples.<ref name=":1" /> |
| + | |||
| + | === Ascending numbers === | ||
| + | In the '''Krshna Yajurveda, Taittriya Aranyaka''', interesting passages containing a sequence of ascending numbers appear in the context of offering venerations to Agni (Deity of Fire) as follows<blockquote>सकृत्ते अग्ने नमः । द्विस्ते नमः । त्रिस्ते नमः । चतुस्ते नमः । पञ्चकृत्वस्ते नमः । दशकृत्वस्ते नम । शतकृत्वस्ते नमः । आसहस्रकृत्वस्ते नमः । अपरिमितकृत्वस्ते नमः । नमस्ते अस्तु मा मा हिँ सीः ३ (Tait. Aran. 4.69)</blockquote>Meaning: O Agni, salutations unto you once, salutations twice, salutations thrice, ...(four, five times). Salutations ten times, hundred times, thousand times. Salutations unto you unlimited times. My venerations to you, never ever hurt me. | ||
| + | |||
| + | === Powers of 10 === | ||
| + | The '''Taittriya Samhita''', presents a list of powers of 10 starting from hundred (10²) to a trillion (10 power 12).<blockquote>शताय स्वाहा सहस्राय स्वाहा । अयुताय स्वाहा नियुताय स्वाहा प्रयुताय स्वाहा । अर्बुदाय स्वाहा न्यर्बुदाय स्वाहा समुद्राय स्वाहा मध्याय स्वाहा । अन्ताय स्वाहा परार्धाय स्वाहा । (Tait. Samh. 7.2.20)<ref>Taittriya Samhita ([https://sa.wikisource.org/wiki/%E0%A4%A4%E0%A5%88%E0%A4%A4%E0%A5%8D%E0%A4%A4%E0%A4%BF%E0%A4%B0%E0%A5%80%E0%A4%AF%E0%A4%B8%E0%A4%82%E0%A4%B9%E0%A4%BF%E0%A4%A4%E0%A4%BE(%E0%A4%B5%E0%A4%BF%E0%A4%B8%E0%A5%8D%E0%A4%B5%E0%A4%B0%E0%A4%83)/%E0%A4%95%E0%A4%BE%E0%A Kanda 7 Prapathaka 2])</ref></blockquote>Meaning: Hail to hundred, ... hail to hundred thousand... hail to hundred million, hail to trillion. | ||
| + | |||
| + | === Odd and Even numbers === | ||
| + | A list of odd numbers and multiples of four occurs in the Taittriya Samhita (4.7.11)<ref>Taittriya Samhita ([https://sa.wikisource.org/wiki/%E0%A4%A4%E0%A5%88%E0%A4%A4%E0%A5%8D%E0%A4%A4%E0%A4%BF%E0%A4%B0%E0%A5%80%E0%A4%AF%E0%A4%B8%E0%A4%82%E0%A4%B9%E0%A4%BF%E0%A4%A4%E0%A4%BE(%E0%A4%B5%E0%A4%BF%E0%A4%B8%E0%A5%8D%E0%A4%B5%E0%A4%B0%E0%A4%83)/%E0%A4%95%E0%A4%BE%E0%A Kanda 4 Anuvaka 7])</ref><blockquote>एका च मे तिस्रश् च मे पञ्च च मे सप्त च मे नव च म एकादश च मे त्रयोदश च मे पञ्चदश च मे सप्तदश च मे नवदश च म...</blockquote><blockquote>मे चतस्रश् च मे ऽष्टौ च मे द्वादश च मे षोडश च मे विꣳशतिश् च मे चतुर्विꣳशतिश् च मे ऽष्टाविꣳशतिश् च मे द्वात्रिꣳशच् च मे...</blockquote>A mention of an interesting number 3339 is seen in the Rigveda, third mandala<blockquote>त्रीणि शता त्री सहस्राण्यग्निं त्रिंशच्च देवा नव चासपर्यन् । औक्षन् घृतैरस्तृणन्बर्हिरस्मा आदिद्धोतारं न्यसादयन्त ॥९॥ (Rig. Veda. 3.9.9)<ref>Rigveda Shakala Samhita ([http://vedicheritage.gov.in/samhitas/rigveda/shakala-samhita/rigveda-shakala-samhita-mandal-03-sukta-009/ Mandala 3 Sukta 3])</ref></blockquote>Here the number 3339 (त्रीणि शता त्री सहस्राण्यग्निं त्रिंशच्च देवा नव) = 33+303+3003 and is also close to 18 years (approx. period of eclipse cycle). | ||
| + | |||
| + | === Multiples of 10 === | ||
| + | In the Rigveda, second mandala we find multiples of ten listed.<blockquote>आ विंशत्या त्रिंशता याह्यर्वाङा चत्वारिंशता हरिभिर्युजानः । आ पञ्चाशता सुरथेभिरिन्द्रा ऽऽषष्ट्या सप्तत्या सोमपेयम् ॥५॥ (Rig. Veda. 2.18.5)</blockquote><blockquote>आशीत्या नवत्या याह्यर्वाङा शतेन हरिभिरुह्यमानः । अयं हि ते... (Rig. Veda. 2.18.6)<ref>Rigveda Shakala Samhita ([http://vedicheritage.gov.in/samhitas/rigveda/shakala-samhita/rigveda-shakala-samhita-mandal-02-sukta-018/ Mandala 2 Sukta 18])</ref></blockquote>Meaning: O Indra, please come with twenty, thirty, forty, horses... with sixty, seventy... carried by hundred horses. | ||
| + | |||
| + | === Notion of Infinite (∞) === | ||
| + | The following widely recited mantra refers to the notion of infinite. | ||
| + | |||
| + | ॐ पूर्णमदः पूर्णमिदं पूर्णात् पूर्णमुदच्यते । पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्यते ॥ | ||
| + | |||
| + | === Fractions === | ||
| + | The Maitrayani Samhita (3.7.7) mentions about several fractions | ||
| + | * 1/16 = Kala (कला) | ||
| + | * 1/12 = Kusht (कुष्ट) | ||
| + | * 1/8 = Shapha (शफः) | ||
| + | * 1/4 = Pada (पदा) | ||
| + | These names of fractions referred in context with bargaining for a price of material (Soma) to be purchased. The price of the material is increased step by step. <blockquote>वसो ह्येष विन्दते यः सोमं क्रीणाति ॥ सोमविक्रयिन्सोतिमं ते क्रीणानि महान्तं बह्वर्हं बहु शोभमानं , कलया ते क्रीणानि, कुष्टया ते क्रीणानि, शफेन ते क्रीणानि, पदा ते क्रीणानि ॥ (Mait. Samh. 3.7.7)<ref>Maitrayani Samhita ([https://sa.wikisource.org/wiki/%E0%A4%AE%E0%A5%88%E0%A4%A4%E0%A5%8D%E0%A4%B0%E0%A4%BE%E0%A4%AF%E0%A4%A3%E0%A5%80%E0%A4%B8%E0%A4%82%E0%A4%B9%E0%A4%BF%E0%A4%A4%E0%A4%BE/%E0%A4%95%E0%A4%BE%E0%A4%A3%E0%A5%8D%E0%A4%A1%E0%A4%82_%E0%A5%A9/%E0%A4%AA%E0%A5%8D%E0%A Kanda 3 Prapathaka 7])</ref></blockquote>Thus we see naming of fractions and operations like sum, subtractions and fractions were quite common at those times.<ref name=":3">Jayashankara, K. (2007) Ph. D. Thesis: ''Sulba sutra, A Critical Analysis.'' Mangalore University ([http://hdl.handle.net/10603/132298 Chapter 8] )</ref> | ||
| + | |||
| + | === Concentric Circles === | ||
| + | Evidence shows that the knowledge of geometry was developed during the vedic period itself. Mantras in Rigveda, for example in Mandala 1 (त्रय: पवयो मधुवाहने रथे । 34.2 and त्रिवन्धुरेण त्रिवृता रथेन त्रिचक्रेण सुवृता । 118.2) there is a mention of three (solid) wheeled, triangular, tricolumnar well-constructed chariot of Ashvini devatas on which they travel. At another instance a wheel formed of hub, spokes and metallic rim are also described. Thus we see that knowledge of construction of drawing concentric circles of desired diameters had developed in the Rigvedic period. The names of Rathakaras that occur in Rigveda are Bhrgu (एवेदिन्द्राय वृषभाय वृष्णे ब्रह्माकर्म भृगवो न रथम् । 4.16.20), Rbhus, Tvastr and others. In Yajurveda the rathakaras are given special importance for their skill. | ||
| + | |||
| + | The knowledge of geometry is also evident from the preparedness to cover wells of different shapes and dimensions.<ref name=":3" /> | ||
| + | |||
| + | == Components of Yajna Vedis == | ||
| + | [[Yajna (यज्ञः)|Yajnas]] are of two main classes: Nitya (obligatory) and Kamya (optional or performed with a special intent). Nitya yajnas are indispensible and not performing them will incur papam (sin) to the yajamana. The Kamya yajnas are, however, optional and those who do not have any specific aims to achieve any desired objects need not perform them. In this section the knowledge of mathematics, the instruments and units of measurements, the bricks used for construction of the altars - as mentioned in Shulbasutras, are discussed. | ||
| + | |||
| + | === चितिः ॥ Chiti === | ||
| + | Every yajna must be carried out in a [[Chiti (चितिः)]] (a fire altar) also called as Vedi, of prescribed shape and size. These sutras give a compilation of principles in geometry that were used in designing the altars where the yajnas were to be performed. The platforms of the altars were built with burnt bricks and mud mortar. It is stated that even a slight irregularity and variation in the form and size of the chiti (Citi) will nullify the object of the whole ritual and may even lead to an adverse effect, accuracy was the key. So ancient adhvaryus took utmost care in building a chiti of right shape and size.<ref name=":0" /> | ||
| + | |||
| + | The chitis had rich symbolic significance and their designs were often intricate. For instance, the Syenacit has the shape of a falcon in flight (a symbolic representation of the aspiration of soaring upward); the Kurmachit is shaped as a tortoise, with extended head and legs, the rathacakracit as a chariot wheel with spokes, and so on.<ref>A. K. Dutta and M. S. Sriram. ''[https://pdfs.semanticscholar.org/bb84/9b5ff23bc22e2056f0aab069c92c05f7af0c.pdf Mathematics and Astronomy in India before 300 BCE.]'' </ref> | ||
| + | |||
| + | === Units of Measurements === | ||
| + | The units of measurement occur commonly in the three vedas themselves; Angula, Gavyuti, Aratni, and Yojana are mentioned in Rigveda, Yojana in Yajurveda and Aratni and Vyama in Atharvaveda. However the length is not clearly mentioned in the samhitas. | ||
| + | |||
| + | 'Angula' seems to be the standard unit for measuring lengths of different vedis, whereas 'purusha' is the standard unit for measuring length of chitis like Syena and others. All other units are derived from Angula. Baudhayana Shulbasutras (1.3-4) while giving the names and definitions of different units begins with the definition of 'Angula'.<blockquote>अथाङ्गुलप्रमाणं चतुर्दशाणवः चतुस्त्रिंशत्तिलाः पृथु संश्लिष्टा इत्यपरम् । (Baud. Shul. Sutr. 1.3)<ref>Baudhayana Shulbasutras ([https://sa.wikisource.org/wiki/%E0%A4%AC%E0%A5%8C%E0%A4%A7%E0%A4%BE%E0%A4%AF%E0%A4%A8%E0%A4%B6%E0%A5%81%E0%A4%B2%E0%A5%8D%E0%A4%AC%E0%A4%B8%E0%A5%82%E0%A4%A4%E0%A5%8D%E0%A4%B0%E0%A4%AE%E0%A5%8D#%E0%A5%A7 Full text])</ref></blockquote> | ||
| + | '''1 Angula (अङ्गुलम्) = 14 Grains of Anu or 34 grains of Tila''' | ||
| + | |||
| + | '''1 Purusha (पुरुषः) = 121 Angulas''' | ||
| + | {| class="wikitable" | ||
| + | |+Derived Units of Measurement in Shulbasutras<ref>Jayashankara, K. (2007) Ph. D. Thesis: ''Sulba sutra, A Critical Analysis.'' Mangalore University ([https://shodhganga.inflibnet.ac.in/bitstream/10603/132298/10/10_chapter%204.pdf Chapter 3] )</ref> | ||
| + | !Reference | ||
| + | !Name | ||
| + | !Measure | ||
| + | |- | ||
| + | |दशाङ्गुलं क्षुद्रपदम् । | ||
| + | |1 Kshudrapada | ||
| + | |10 Angulas | ||
| + | |- | ||
| + | |द्वादश प्रादेशः । | ||
| + | |1 Pradesha | ||
| + | |12 Angula | ||
| + | |- | ||
| + | | rowspan="2" |पृथोत्तरयुगेत्रयोदशिके। | ||
| + | |1 Prth | ||
| + | | rowspan="2" |13 Angula | ||
| + | |- | ||
| + | |1 Uttarayayuga | ||
| + | |- | ||
| + | |पदं पञ्चदश । | ||
| + | |1 Pada | ||
| + | |15 Angula | ||
| + | |- | ||
| + | |द्विपदः प्रक्रमः । | ||
| + | |1 Prakrama (2 Padas) | ||
| + | |30 Angula | ||
| + | |- | ||
| + | |द्वौ प्रादेशावरत्निः । | ||
| + | |1 Aratni (2 Pradesha) | ||
| + | |24 Angula | ||
| + | |- | ||
| + | |द्वात्रिंश्ज्जानुः । | ||
| + | |1 Janu | ||
| + | |32 Angula | ||
| + | |- | ||
| + | | rowspan="2" |षटि्त्रंशच्छम्याबाहू । | ||
| + | |1 Shamya | ||
| + | | rowspan="2" |36 Angula | ||
| + | |- | ||
| + | |1 Bahu | ||
| + | |- | ||
| + | | rowspan="2" |पञ्चारत्निः पुरुषो व्यामश्च । | ||
| + | |1 Purusha (5 Aratni) | ||
| + | | rowspan="2" |121 Angula | ||
| + | |- | ||
| + | |1 Vyama (5 Aratni) | ||
| + | |- | ||
| + | |चतुररत्निव्व्या यामः। | ||
| + | |1 Yama | ||
| + | |98 Angula | ||
| + | |- | ||
| + | |अष्टाशीतिशतमीषा । | ||
| + | |1 Isha | ||
| + | |188 Angula | ||
| + | |- | ||
| + | |चतुःशतमक्षः । | ||
| + | |1 Aksha | ||
| + | |104 Angula | ||
| + | |- | ||
| + | |षडशीतिर्युगम् । | ||
| + | |1 Yuga | ||
| + | |86 Angula | ||
| + | |} | ||
| + | It gives us an insight about how our ancients developed units of measurement long before other civilizations mentioned it. However, it should also be remembered that the Shulbasutras of different Sutrakaras have slight variations thus we see versions of the above angula measures. It cannot be more emphasized that later day developments in such areas of ganita are founded on these ancient works. | ||
| + | |||
| + | == Subject-matter of Shulbasutras == | ||
| + | Baudhayana shulbasutras are considered to be the most ancient of the Shulbasutra texts. It also presents a very systematic and detailed treatment of several topics that are skipped in later texts. | ||
| + | {| class="wikitable" | ||
| + | |+Topics covered in Baudhayana Shulbasutra<ref name=":1" /> | ||
| + | ! | ||
| + | !Topics | ||
| + | !English Equivalent | ||
| + | |- | ||
| + | |1 | ||
| + | |रेखामानपरिभाषा | ||
| + | |Units of linear measurement | ||
| + | |- | ||
| + | |2 | ||
| + | |चतुरश्रकरणोपायः | ||
| + | |Construction of squares, rectangles, etc | ||
| + | |- | ||
| + | |3 | ||
| + | |करण्यानयनम् | ||
| + | |Obtaining the surds/theorem of the square og the diagonal | ||
| + | |- | ||
| + | |4 | ||
| + | |क्षेत्राकारपरिणामः | ||
| + | |Transformation of geometrical figures | ||
| + | |- | ||
| + | |5 | ||
| + | |नानाविधवेदिविहरणम् | ||
| + | |Plan for different sacrificial grounds (darsa, pasubandha, sutramani, agnistoma etc) | ||
| + | |- | ||
| + | |6 | ||
| + | |अग्नीनां प्रमाणक्षेत्रमानम् | ||
| + | |Areas of the sacrificial agnis/vedis | ||
| + | |- | ||
| + | |7 | ||
| + | |इष्टकसङ्ख्यापरिमाणादिकथनम् | ||
| + | |Specifying the number of bricks used on the construction of vedis including their sizes and shapes | ||
| + | |- | ||
| + | |8 | ||
| + | |इष्टकोपधाने रीत्यादिनिर्णयः | ||
| + | |Choosing clay, sand, etc in making bricks | ||
| + | |- | ||
| + | |9 | ||
| + | |इष्टकोपधानप्रकारः | ||
| + | |Process of manufacturing the bricks | ||
| + | |- | ||
| + | |10 | ||
| + | |श्येनचिदाद्याकारनिरुपणम् | ||
| + | |Describing the shapes of syenachiti | ||
| + | |} | ||
| + | |||
| + | == Mathematical Topics in Shulbasutras == | ||
| + | A brief explanation of a few mathematical topics dealt in the shulbasutras is given below | ||
| + | |||
| + | === Approximation of Surds === | ||
| + | Besides presenting the details related to the construction of altars - that generally possess a bilateral symmetry - the Shulbasutra texts also present different interesting approximations for surds. The motivation for presenting estimates of surds could be traced to the attempts of vedic priests | ||
| + | * to solve the problem of 'squaring a circle' and vice versa | ||
| + | * to construct a square whose area is n times the area of a given square, and so on | ||
| + | |||
| + | === Determination of cardinal directions === | ||
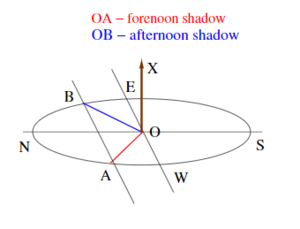
| + | [[File:Determining Cardinal Directions.PNG|thumb|Determination of Cardinal Directions]] | ||
| + | Determining the exact east-west line at a given location is a prerequisite for all constructions, be it a residence, a temple, a vedi or yajna kunda. Finding the cardinal directions using a shanku has been described thus:<ref name=":1" /><blockquote>समे शंङ्कु निखाय शंङ्कुसम्मितया रज्ज्वा मण्डलं परिलिख्य यत्र लेखयोः शंङ्क्वग्रच्छाया निपतति तत्र शंङ्कू निहन्ति सा प्राची । (Katy. Shul. Sutr. 1.2)</blockquote>Fixing a pin (or gnomon) on levelled ground and drawing a circle with a cord measured by the gnomon, he fixes pins at points on the line of the circumference where the shadow of the tip of the gnomon falls. That gives the east-west line (prachi). | ||
| + | |||
| + | Now, to answer the question about the necessity of such an experiment, instead of simply looking at the sunrise or sunset to determine the cardinal directions, the commentator Mahidhara observes:<blockquote>... तस्य उदयस्थानानां बहुत्वात् प्रतिदिनं भिन्नत्वात् अनियमेन प्राची ज्ञातुं न शक्या। तस्मात् शङ्कुस्थापनेन प्राचीसाधनमुक्तम्। दक्षिणायने चित्रापर्यन्तमर्कोऽभ्युदेति। मेषतुलासङ्क्रात्यहे प्राच्यां शुद्धायामुदेति। ततोऽर्कात् प्रचीज्ञानं दुर्घटम्।</blockquote>Meaning: Since the rising points are many, varying from day to day, the (cardinal) east point cannot be known (from the sunrise point). Therefore it has been prescribed that the east be determined by fixing a Shanku (शङ्कु)... therefore simply looking at the sun and determining the east is difficult. | ||
| + | |||
| + | Having obtained the prachi, getting udichi (the north-south line) correctly is extremely important for the construction of various vedis having bilateral symmetry. Two methods have been described for obtaining the perpendicular bisector of a given straight line:<ref name=":1" /> | ||
| + | * रज्ज्वभ्यासनम् । folding the cord | ||
| + | * मत्स्यचित्रणम् । drawing fish-figure | ||
| + | Katyayana Shulbasutra (1.3) describes these methods in detail to determine the north-south line using the shanku. Thus accurate determination of simple geometric figures was perfected using simple tools such as a gnomon and cords. | ||
| − | + | === Construction of a Square === | |
| + | Altars for the conduct of yajnas required the vedis, kundas in which Agni is maintained for performing oblations. There are multitude of the altars of the Nityaagni, the Tretagni (Garhapatya, Ahavaniya and Dakshinagni) in which the Shrauta karmas are performed. Other Grhyakarmas are performed in Ekagni or Aupasanagni. | ||
| − | + | Now from the Shulbasutras, we learn that the altar of Garhapatya agni should be in the form of a square, according to one school and a circle according to a different school. The altar for the Ahavaniya agni should always be square and that of the Dakshinagni semi-circular. The area of each, however, must be the same and equal to one square vyaama (1 vyaama = 96 angulis). So the construction of these three altars, as evident, pre-supposes the knowledge of the following geometrical operations: | |
| + | # To construct a square on a given straight line | ||
| + | # To circle a square and vice versa | ||
| + | # To double a circle | ||
== References == | == References == | ||
Latest revision as of 14:46, 16 April 2020
Shulbasutras (Samskrit: शुल्बसूत्राणि) are manuals for the construction of yajnas. They are sections of the Kalpasutras, associated in particular with the Shrautasutras. Each Shrautasutra seemed to have their own Shulbasutra section based on literary data; however, in the present days, only seven of these sutra works, Baudhayana, Apastamba, Katyayana, Manava, Maitayana, Varaha and Vadhula are available.
परिचयः ॥ Introduction
Recognized as the oldest and earliest treatises on mathematical problems, Shulbasutras give us a glimpse of the knowledge of geometry that the vedic people possessed. Incidentally they furnish us with a few other subjects of much mathematical interest.[1]
One of the prime occupations of the vedic people, performing yajnas, required altars or yajna-vedis of prescribed shapes and sizes. It was primarily in connection with the construction of altars that problems of geometry and also of arithmetic and algebra presented themselves to these ancient rshis, which led to the development of these texts.
Authors and Commentators
Unlike the other Sutra charanas, there are a very few Shulbasutra texts available at present and all of them belong to Yajurveda. The Shulbasutras of Baudhayana, Apastamba, Katyayana and Manava are the main sources of the knowledge of geometry. The Kalpa texts of Vedangas clearly outline that astronomy on one hand and geometry on the other were cultivated under different circumstances by different rtviks based on the duties apportioned to them in the conduct of yajnas.[2][1]
List of Shulbasutra Works
Of the available extant texts, Baudhayana Shulbasutra is considered to be the most ancient one. Following is the list of shulbasutras and their commentators.
| Vedas | Shakas | Shulbasutra | Contents | Commentators |
|---|---|---|---|---|
| Rigveda | Shakala | None available | ||
| Kaushitaki | ||||
| Shukla Yajurveda | Vajasaneya | Katyayana | Purvabhaga (7 Kandikas with 90 Sutras)
Uttarabhaga (40 or 48 shlokas) |
Rama or Ramachandra (Shulba-sutra-vrtti), Shulbasutravivarana (Mahidhara), Karka (Shulbasutrabhashya) |
| Krishna Yajurveda | Taittriya | Baudhayana | 3 Adhyayas (about 520 Sutras) | Dvarakanatha Yajva (Sulba-dipika), Venkatesvara Dikshita (Shulba-mimamsa) |
| Apastamba | 6 Patalas (21 Adhyayas and 223 Sutras) | Kapardisvami (Shulba-vyakhya), Karavindasvami (Shulba-pradipika), Sundararaja (Shulba-pradipa or Sundararajiya), Gopala (Shulbabhashya) | ||
| Varaha | 3 Adhyayas | |||
| Hiranyakeshi | ||||
| Vadhula | Vadhula (वाधूलः) | |||
| Maitrayani | Manava by Manu | 7 Khandas | Narada | |
| Maitrayana | 4 Khandas | Shankarabhatta | ||
| Samaveda | Kauthuma | None available | ||
| Rananiya | ||||
| Jaimini | ||||
| Atharvaveda | None available | |||
Qualities of a Shulbakara
Mahidhara in his commentary on Katyayana shulbasutra succintly describes the qualities of a Shulbakara.[3]
सङ्ख्याज्ञः परिमाणज्ञः समसूत्रनिरञ्छकः । समसूत्रौ भवेद्विद्वान् शुल्बवित् परिपृच्छकः।।
शास्त्रबुद्धिविभागज्ञः परशास्त्रकुतूहलः। शिल्पिभ्यः स्थपतिभ्यश्चाप्याददीत मतीः सदा।।
तिर्यङ्मान्याश्च सर्वार्थः पार्श्वमान्याश्च योगवित्। करणीनां विभागज्ञः नित्योद्युक्तश्च सर्वदा।।
A shulbakara must be versed in arithmetic, versed in mensuration, must be an inquirer, quite knowledgeable in one's own discipline, must be enthusiastic in learning other disciplines, always willing to learn from practicing sculptors and architects... and one who is always industrious.
Besides having the above qualities, Shulbakaras had to perform several other important duties systematically viz.,
- to clean and level a plot on which the altar is to be constructed
- to fix the east-west line (prachi) for it was considered as the reference line
- to construct bricks of specific sizes
- to draw diagrams of specific sizes on the level ground on which the altar is to be constructed
- to lay bricks subject to certain principles
व्युत्पत्तिः॥ Etymology
The word Shulba (शुल्ब) means a 'cord', 'a rope', 'a string'. A Sutra refers to a short rule. The commentators refer to this subject matter as Shulba as the true name, Shulba-parishista, Shulbi Kriya etc.
In few other instances the word "rajju (रज्जुः) has been used. B. B. Datta states that the words "shulba (शुल्ब)" "shulva (शुल्व)" and "rajju (रज्जुः) may be used synonymously to mean a rope or cord.[1]
The word "shulba or shulva" (sulva) stems from the dhatu "शुल्ब्" used in the meaning "माने । to measure" and hence its etymological significance is "measuring" or act of measurement. The term Shulba can be presented in the following ways[3]
- भावव्युत्पत्तिः - शुल्बनम् इति शुल्बः । the act of measuring (mensuration)
- कर्मव्युत्पत्तिः - शुल्बयते इति शुल्बः । the entity/result obtained by measuring (line)
- करणव्युत्पत्तिः - शुल्बयत्यनेन इति शुल्बः । the instrument of measuring
In the Shulbas the measuring tape is called "Rajju", so is "a line". One who is well-versed in the science of Shulba (geometry) is called Shulbavijnana, a Shulbavid (expert in geometry), a Sulbapariprcchaka (an inquirer into the Shulba), a Samkhyaajna (expert in numbers), Parimaanajna (expert in measuring). A special term sama-sutra-niranchaka (meaning uniform rope stretcher) is also used, this rope plays a very significant role and we find many references of similar words rajjuka, rakku-grahaka, sutra-grahaka - all used to denote a maharaja's land surveyor. A sutra-grahaka is further described as an expert in alignment, a rekajna, one who knows "the line".[1]
It is extremely interesting to note that land surveying is an ancient procedure followed by our ancestors.
Mathematical References in Vedas
The existence of numbers, their usage, the decimal system being in vogue, the concept of infinity are unambiguously presented in the following examples.[3]
Ascending numbers
In the Krshna Yajurveda, Taittriya Aranyaka, interesting passages containing a sequence of ascending numbers appear in the context of offering venerations to Agni (Deity of Fire) as follows
सकृत्ते अग्ने नमः । द्विस्ते नमः । त्रिस्ते नमः । चतुस्ते नमः । पञ्चकृत्वस्ते नमः । दशकृत्वस्ते नम । शतकृत्वस्ते नमः । आसहस्रकृत्वस्ते नमः । अपरिमितकृत्वस्ते नमः । नमस्ते अस्तु मा मा हिँ सीः ३ (Tait. Aran. 4.69)
Meaning: O Agni, salutations unto you once, salutations twice, salutations thrice, ...(four, five times). Salutations ten times, hundred times, thousand times. Salutations unto you unlimited times. My venerations to you, never ever hurt me.
Powers of 10
The Taittriya Samhita, presents a list of powers of 10 starting from hundred (10²) to a trillion (10 power 12).
शताय स्वाहा सहस्राय स्वाहा । अयुताय स्वाहा नियुताय स्वाहा प्रयुताय स्वाहा । अर्बुदाय स्वाहा न्यर्बुदाय स्वाहा समुद्राय स्वाहा मध्याय स्वाहा । अन्ताय स्वाहा परार्धाय स्वाहा । (Tait. Samh. 7.2.20)[4]
Meaning: Hail to hundred, ... hail to hundred thousand... hail to hundred million, hail to trillion.
Odd and Even numbers
A list of odd numbers and multiples of four occurs in the Taittriya Samhita (4.7.11)[5]
एका च मे तिस्रश् च मे पञ्च च मे सप्त च मे नव च म एकादश च मे त्रयोदश च मे पञ्चदश च मे सप्तदश च मे नवदश च म...
मे चतस्रश् च मे ऽष्टौ च मे द्वादश च मे षोडश च मे विꣳशतिश् च मे चतुर्विꣳशतिश् च मे ऽष्टाविꣳशतिश् च मे द्वात्रिꣳशच् च मे...
A mention of an interesting number 3339 is seen in the Rigveda, third mandala
त्रीणि शता त्री सहस्राण्यग्निं त्रिंशच्च देवा नव चासपर्यन् । औक्षन् घृतैरस्तृणन्बर्हिरस्मा आदिद्धोतारं न्यसादयन्त ॥९॥ (Rig. Veda. 3.9.9)[6]
Here the number 3339 (त्रीणि शता त्री सहस्राण्यग्निं त्रिंशच्च देवा नव) = 33+303+3003 and is also close to 18 years (approx. period of eclipse cycle).
Multiples of 10
In the Rigveda, second mandala we find multiples of ten listed.
आ विंशत्या त्रिंशता याह्यर्वाङा चत्वारिंशता हरिभिर्युजानः । आ पञ्चाशता सुरथेभिरिन्द्रा ऽऽषष्ट्या सप्तत्या सोमपेयम् ॥५॥ (Rig. Veda. 2.18.5)
आशीत्या नवत्या याह्यर्वाङा शतेन हरिभिरुह्यमानः । अयं हि ते... (Rig. Veda. 2.18.6)[7]
Meaning: O Indra, please come with twenty, thirty, forty, horses... with sixty, seventy... carried by hundred horses.
Notion of Infinite (∞)
The following widely recited mantra refers to the notion of infinite.
ॐ पूर्णमदः पूर्णमिदं पूर्णात् पूर्णमुदच्यते । पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्यते ॥
Fractions
The Maitrayani Samhita (3.7.7) mentions about several fractions
- 1/16 = Kala (कला)
- 1/12 = Kusht (कुष्ट)
- 1/8 = Shapha (शफः)
- 1/4 = Pada (पदा)
These names of fractions referred in context with bargaining for a price of material (Soma) to be purchased. The price of the material is increased step by step.
वसो ह्येष विन्दते यः सोमं क्रीणाति ॥ सोमविक्रयिन्सोतिमं ते क्रीणानि महान्तं बह्वर्हं बहु शोभमानं , कलया ते क्रीणानि, कुष्टया ते क्रीणानि, शफेन ते क्रीणानि, पदा ते क्रीणानि ॥ (Mait. Samh. 3.7.7)[8]
Thus we see naming of fractions and operations like sum, subtractions and fractions were quite common at those times.[9]
Concentric Circles
Evidence shows that the knowledge of geometry was developed during the vedic period itself. Mantras in Rigveda, for example in Mandala 1 (त्रय: पवयो मधुवाहने रथे । 34.2 and त्रिवन्धुरेण त्रिवृता रथेन त्रिचक्रेण सुवृता । 118.2) there is a mention of three (solid) wheeled, triangular, tricolumnar well-constructed chariot of Ashvini devatas on which they travel. At another instance a wheel formed of hub, spokes and metallic rim are also described. Thus we see that knowledge of construction of drawing concentric circles of desired diameters had developed in the Rigvedic period. The names of Rathakaras that occur in Rigveda are Bhrgu (एवेदिन्द्राय वृषभाय वृष्णे ब्रह्माकर्म भृगवो न रथम् । 4.16.20), Rbhus, Tvastr and others. In Yajurveda the rathakaras are given special importance for their skill.
The knowledge of geometry is also evident from the preparedness to cover wells of different shapes and dimensions.[9]
Components of Yajna Vedis
Yajnas are of two main classes: Nitya (obligatory) and Kamya (optional or performed with a special intent). Nitya yajnas are indispensible and not performing them will incur papam (sin) to the yajamana. The Kamya yajnas are, however, optional and those who do not have any specific aims to achieve any desired objects need not perform them. In this section the knowledge of mathematics, the instruments and units of measurements, the bricks used for construction of the altars - as mentioned in Shulbasutras, are discussed.
चितिः ॥ Chiti
Every yajna must be carried out in a Chiti (चितिः) (a fire altar) also called as Vedi, of prescribed shape and size. These sutras give a compilation of principles in geometry that were used in designing the altars where the yajnas were to be performed. The platforms of the altars were built with burnt bricks and mud mortar. It is stated that even a slight irregularity and variation in the form and size of the chiti (Citi) will nullify the object of the whole ritual and may even lead to an adverse effect, accuracy was the key. So ancient adhvaryus took utmost care in building a chiti of right shape and size.[1]
The chitis had rich symbolic significance and their designs were often intricate. For instance, the Syenacit has the shape of a falcon in flight (a symbolic representation of the aspiration of soaring upward); the Kurmachit is shaped as a tortoise, with extended head and legs, the rathacakracit as a chariot wheel with spokes, and so on.[10]
Units of Measurements
The units of measurement occur commonly in the three vedas themselves; Angula, Gavyuti, Aratni, and Yojana are mentioned in Rigveda, Yojana in Yajurveda and Aratni and Vyama in Atharvaveda. However the length is not clearly mentioned in the samhitas.
'Angula' seems to be the standard unit for measuring lengths of different vedis, whereas 'purusha' is the standard unit for measuring length of chitis like Syena and others. All other units are derived from Angula. Baudhayana Shulbasutras (1.3-4) while giving the names and definitions of different units begins with the definition of 'Angula'.
अथाङ्गुलप्रमाणं चतुर्दशाणवः चतुस्त्रिंशत्तिलाः पृथु संश्लिष्टा इत्यपरम् । (Baud. Shul. Sutr. 1.3)[11]
1 Angula (अङ्गुलम्) = 14 Grains of Anu or 34 grains of Tila
1 Purusha (पुरुषः) = 121 Angulas
| Reference | Name | Measure |
|---|---|---|
| दशाङ्गुलं क्षुद्रपदम् । | 1 Kshudrapada | 10 Angulas |
| द्वादश प्रादेशः । | 1 Pradesha | 12 Angula |
| पृथोत्तरयुगेत्रयोदशिके। | 1 Prth | 13 Angula |
| 1 Uttarayayuga | ||
| पदं पञ्चदश । | 1 Pada | 15 Angula |
| द्विपदः प्रक्रमः । | 1 Prakrama (2 Padas) | 30 Angula |
| द्वौ प्रादेशावरत्निः । | 1 Aratni (2 Pradesha) | 24 Angula |
| द्वात्रिंश्ज्जानुः । | 1 Janu | 32 Angula |
| षटि्त्रंशच्छम्याबाहू । | 1 Shamya | 36 Angula |
| 1 Bahu | ||
| पञ्चारत्निः पुरुषो व्यामश्च । | 1 Purusha (5 Aratni) | 121 Angula |
| 1 Vyama (5 Aratni) | ||
| चतुररत्निव्व्या यामः। | 1 Yama | 98 Angula |
| अष्टाशीतिशतमीषा । | 1 Isha | 188 Angula |
| चतुःशतमक्षः । | 1 Aksha | 104 Angula |
| षडशीतिर्युगम् । | 1 Yuga | 86 Angula |
It gives us an insight about how our ancients developed units of measurement long before other civilizations mentioned it. However, it should also be remembered that the Shulbasutras of different Sutrakaras have slight variations thus we see versions of the above angula measures. It cannot be more emphasized that later day developments in such areas of ganita are founded on these ancient works.
Subject-matter of Shulbasutras
Baudhayana shulbasutras are considered to be the most ancient of the Shulbasutra texts. It also presents a very systematic and detailed treatment of several topics that are skipped in later texts.
| Topics | English Equivalent | |
|---|---|---|
| 1 | रेखामानपरिभाषा | Units of linear measurement |
| 2 | चतुरश्रकरणोपायः | Construction of squares, rectangles, etc |
| 3 | करण्यानयनम् | Obtaining the surds/theorem of the square og the diagonal |
| 4 | क्षेत्राकारपरिणामः | Transformation of geometrical figures |
| 5 | नानाविधवेदिविहरणम् | Plan for different sacrificial grounds (darsa, pasubandha, sutramani, agnistoma etc) |
| 6 | अग्नीनां प्रमाणक्षेत्रमानम् | Areas of the sacrificial agnis/vedis |
| 7 | इष्टकसङ्ख्यापरिमाणादिकथनम् | Specifying the number of bricks used on the construction of vedis including their sizes and shapes |
| 8 | इष्टकोपधाने रीत्यादिनिर्णयः | Choosing clay, sand, etc in making bricks |
| 9 | इष्टकोपधानप्रकारः | Process of manufacturing the bricks |
| 10 | श्येनचिदाद्याकारनिरुपणम् | Describing the shapes of syenachiti |
Mathematical Topics in Shulbasutras
A brief explanation of a few mathematical topics dealt in the shulbasutras is given below
Approximation of Surds
Besides presenting the details related to the construction of altars - that generally possess a bilateral symmetry - the Shulbasutra texts also present different interesting approximations for surds. The motivation for presenting estimates of surds could be traced to the attempts of vedic priests
- to solve the problem of 'squaring a circle' and vice versa
- to construct a square whose area is n times the area of a given square, and so on
Determination of cardinal directions
Determining the exact east-west line at a given location is a prerequisite for all constructions, be it a residence, a temple, a vedi or yajna kunda. Finding the cardinal directions using a shanku has been described thus:[3]
समे शंङ्कु निखाय शंङ्कुसम्मितया रज्ज्वा मण्डलं परिलिख्य यत्र लेखयोः शंङ्क्वग्रच्छाया निपतति तत्र शंङ्कू निहन्ति सा प्राची । (Katy. Shul. Sutr. 1.2)
Fixing a pin (or gnomon) on levelled ground and drawing a circle with a cord measured by the gnomon, he fixes pins at points on the line of the circumference where the shadow of the tip of the gnomon falls. That gives the east-west line (prachi). Now, to answer the question about the necessity of such an experiment, instead of simply looking at the sunrise or sunset to determine the cardinal directions, the commentator Mahidhara observes:
... तस्य उदयस्थानानां बहुत्वात् प्रतिदिनं भिन्नत्वात् अनियमेन प्राची ज्ञातुं न शक्या। तस्मात् शङ्कुस्थापनेन प्राचीसाधनमुक्तम्। दक्षिणायने चित्रापर्यन्तमर्कोऽभ्युदेति। मेषतुलासङ्क्रात्यहे प्राच्यां शुद्धायामुदेति। ततोऽर्कात् प्रचीज्ञानं दुर्घटम्।
Meaning: Since the rising points are many, varying from day to day, the (cardinal) east point cannot be known (from the sunrise point). Therefore it has been prescribed that the east be determined by fixing a Shanku (शङ्कु)... therefore simply looking at the sun and determining the east is difficult.
Having obtained the prachi, getting udichi (the north-south line) correctly is extremely important for the construction of various vedis having bilateral symmetry. Two methods have been described for obtaining the perpendicular bisector of a given straight line:[3]
- रज्ज्वभ्यासनम् । folding the cord
- मत्स्यचित्रणम् । drawing fish-figure
Katyayana Shulbasutra (1.3) describes these methods in detail to determine the north-south line using the shanku. Thus accurate determination of simple geometric figures was perfected using simple tools such as a gnomon and cords.
Construction of a Square
Altars for the conduct of yajnas required the vedis, kundas in which Agni is maintained for performing oblations. There are multitude of the altars of the Nityaagni, the Tretagni (Garhapatya, Ahavaniya and Dakshinagni) in which the Shrauta karmas are performed. Other Grhyakarmas are performed in Ekagni or Aupasanagni.
Now from the Shulbasutras, we learn that the altar of Garhapatya agni should be in the form of a square, according to one school and a circle according to a different school. The altar for the Ahavaniya agni should always be square and that of the Dakshinagni semi-circular. The area of each, however, must be the same and equal to one square vyaama (1 vyaama = 96 angulis). So the construction of these three altars, as evident, pre-supposes the knowledge of the following geometrical operations:
- To construct a square on a given straight line
- To circle a square and vice versa
- To double a circle
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Datta. Bibhutibhusan, (1932) The Science of the Sulba. A Study in Early Hindu Geometry. Calcutta: The University of Calcutta
- ↑ Bag, A. K., (1979) Mathematics in Ancient and Medieval India. Varanasi: Chaukhambha Orientalia. (Pages 103 - 174)
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Prof. K. Ramasubramaniam's Lectures - Vedas and Sulbasutras, Parts 1 and 2
- ↑ Taittriya Samhita (Kanda 7 Prapathaka 2)
- ↑ Taittriya Samhita (Kanda 4 Anuvaka 7)
- ↑ Rigveda Shakala Samhita (Mandala 3 Sukta 3)
- ↑ Rigveda Shakala Samhita (Mandala 2 Sukta 18)
- ↑ Maitrayani Samhita (Kanda 3 Prapathaka 7)
- ↑ 9.0 9.1 Jayashankara, K. (2007) Ph. D. Thesis: Sulba sutra, A Critical Analysis. Mangalore University (Chapter 8 )
- ↑ A. K. Dutta and M. S. Sriram. Mathematics and Astronomy in India before 300 BCE.
- ↑ Baudhayana Shulbasutras (Full text)
- ↑ Jayashankara, K. (2007) Ph. D. Thesis: Sulba sutra, A Critical Analysis. Mangalore University (Chapter 3 )