Difference between revisions of "Area (क्षेत्रफल)"
(Adding Content) |
(Adding image and editing) |
||
| Line 2: | Line 2: | ||
उदाहारण | उदाहारण | ||
| + | * Square | ||
| + | [[File:Square.PNG|left|thumb|256x256px]] | ||
| + | Area = 25 x 25 | ||
| − | + | = 625unit<sup>2</sup> | |
| + | |||
| + | * Rhombus | ||
| + | Area = Diagonal multiplication | ||
2 | 2 | ||
= 30 x 40= 600 unit2 | = 30 x 40= 600 unit2 | ||
Revision as of 16:14, 21 February 2019
भारतीय दर्शन ग्रन्थों से प्रेरित हमारे पूर्वाचार्यों ने गणित-शास्त्र के लेखन में भी प्रमेय विषयों पर अधिक ध्यान दिया है। इन आचार्यों की लेखन-शैली से यह प्रतीत होता है।
चतुर्भुजस्यानियतौ हि कर्णो कथं ततोऽस्मिन्नियतं फलं स्यात्।
प्रसाधितौ तच्छ्रवणौ यदाद्यै: स्वकाल्पितौ तावितस्त्र न स्त:।।
तेष्वेव बाहुष्वपरौ च कर्णावनेकधा श्रेत्रफलं ततश्च।
लीलावती ग्रन्थ में भास्कराचार्य 'श्रेत्रफल विचार करते समय श्रेत्रव्यवहार में यह विषय विस्तार से प्रस्तुत करते हैं। किसी भी श्रेत्र (figure) में उसके कर्ण (Diagonal) अथवा लम्ब (perpendicular) के ज्ञान बिना उस श्रेत्र का फल सम्बन्धी विचार सर्वथा उचित नहीं है। यद्यपि पूर्वाचार्यो ने स्वकल्पित कर्ण का साधन किया, परन्तु वे कर्ण अन्य जगह नहीं हो सकते। क्योंकि उन्ही भुजाओं पर से अनेक कर्ण और उन कर्णों पर आधारित अनेक फल होते है। इस शाब्दिक चर्चा को हम आकृति द्वारा समझने का प्रयास करते है।
उदाहारण
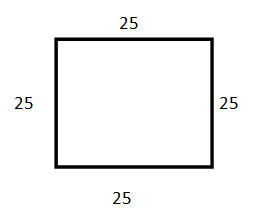
- Square
Area = 25 x 25
= 625unit2
- Rhombus
Area = Diagonal multiplication
2
= 30 x 40= 600 unit2